python绘制参数方程的动画

Posted on | | 次

© 2018 *All rights reserved by liudx .:smile:

​ Python的matplotlib是一个功能强大的绘图库，可以很方便的绘制数学图形。官方给出了很多简单的实例，结合中文翻译的示例Tutorial，可以满足日常工作的大部分需求了。但是实际工作中，一些有趣的东西很难使用常规方程（笛卡尔坐标和极坐标）方式绘制，事实上，大部分工程上都是使用参数方程来描述曲线。本文给出一些参数方程绘制的实例，之后会扩展为动画形式绘制，可以看到这些复杂的方程是如何简单优美的绘制出来。

1 参数方程绘制

​ 首先介绍下椭圆的参数方程：

$$
\begin{cases}
x = a \cdot \cos(t)\\
y = b \cdot \sin(t)
\end{cases}
$$

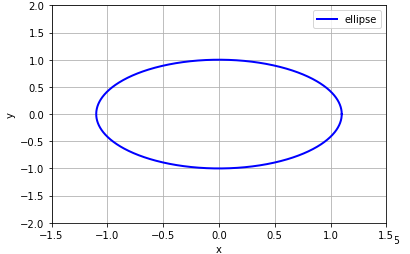
​ 其中$a,b$分别是椭圆的长轴、短轴。绘制椭圆的python代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import matplotlib.pyplot as plt
import numpy as np  

fig = plt.figure()
ax = plt.gca()
#椭圆参数方程
r1 = 1.1
r2 = 1
t = np.linspace(0, np.pi*2, 1000) # 生成参数t的数组
x = r1 * np.cos(t)
y = r2 * np.sin(t)
plt.plot(x, y, color='blue', linewidth=2, label='ellipse')  
plt.xlabel('x')  
plt.ylabel('y')  
plt.ylim(-2, 2)  
plt.xlim(-1.5,1.5)
ax.grid()
plt.show()

​ 结果如下:

​

​ 下面我们来个复杂点的例子，绘制炮弹的弹道曲线（当然是理想情况的），我们先根据公式推算一把，首先我们设炮弹出口速度$v_0(m/s)$,向上仰角为$\theta$ °，时间为$t(s)$, 大炮的筒口初始坐标初始为(0,0)，则有：

$$
\begin{cases}
x=v_0\cdot\sin(\theta)\cdot t \\
y=v_0\cdot\cos(\theta)\cdot t - v_0\cdot\cos(\theta)\cdot g \cdot t^2
\end{cases}
$$

​ 对应python代码為：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def Parabolic(v0, theta_x): # 模拟炮弹飞行曲线
    g = 9.80665 # m/s^2
    v0_x = v0*np.cos(theta_x)
    v0_y = v0*np.sin(theta_x)
    t_m = (v0_y / g) # 飞行时间
    #h = g*t_m**2/2
    t = np.linspace(0, v0_x * t_m * 2, v0*1000)
    x = v0_x * t
    y = v0_y *t - v0_y *g * t**2 / 2
    return x,y
    
if __name__ == '__main__':
    linestyles = ['-', '--', '-.', ':']
    x1, y1 = Parabolic(100, np.deg2rad(45))
    x2, y2 = Parabolic(100, np.deg2rad(30))
    x3, y3 = Parabolic(100, np.deg2rad(60))
    plt.plot(x1, y1, color='r', linewidth=1, linestyle="--",label='45deg')
    plt.plot(x2, y2, color='y', linewidth=1, linestyle="-.", label='30deg')
    plt.plot(x3, y3, color='c', linewidth=1, linestyle=":", label='60deg')
    plt.xlabel('x')
    plt.ylabel('h')
    
    plt.xlim(0, 20)
    plt.ylim(0, 8)
    plt.legend(loc='upper center') 
    plt.show()

​ 为了方便示意，我分别绘制了初速为$100m/s$时，仰角为45°、30°、60°的炮弹落地曲线：

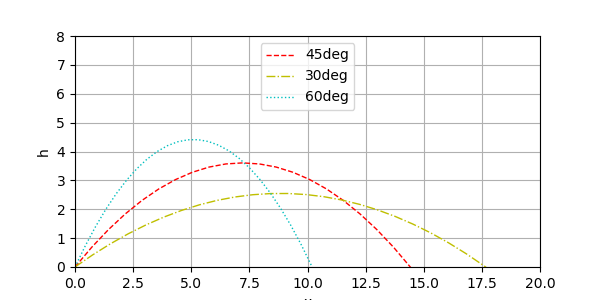
​ 验证了我们高中物理中的一个结论：这货不就是抛物线嘛。

2 动画animation

​ 看完静态的参数方程，还是不过瘾，我们来做个动画玩玩。首先是绘制一个内旋轮，引用下这位老哥的例子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import numpy as np 
import matplotlib
import matplotlib.pyplot as plt 
import matplotlib.animation as animation
fig = plt.figure(figsize=(6, 6)) # 图像大小
ax = plt.gca()
ax.grid()
ln1, = ax.plot([], [], '-', color='b', lw=2) # 注意逗号，取出plot数据:plot return A list of Line2D objects representing the plotted data.
ln2, = ax.plot([], [], '-', color='r', lw=1)
theta = np.linspace(0, 2*np.pi, 100) # 参数t的数组
r_out = 1 # 静态圆的半径
r_in = 0.5 # 动态圆的半径

def init():
    ax.set_xlim(-2, 2)
    ax.set_ylim(-2, 2)
    x_out = [r_out*np.cos(theta[i]) for i in range(len(theta))]
    y_out = [r_out*np.sin(theta[i]) for i in range(len(theta))]
    ln1.set_data(x_out, y_out) # 静圆
    return ln1, # 此处返回tuple

def update(i): # 每次回调时，传入索引`0~range(len(theta))`,注意repeat时索引会归0
    x_in = [(r_out-r_in)*np.cos(theta[i])+r_in*np.cos(theta[j]) for j in range(len(theta))]
    y_in = [(r_out-r_in)*np.sin(theta[i])+r_in*np.sin(theta[j]) for j in range(len(theta))]
    ln2.set_data(x_in, y_in) # 动圆
    return ln2,

ani = animation.FuncAnimation(fig, update, range(len(theta)), init_func=init, interval=30)
#ani.save('roll.gif', writer='imagemagick', fps=100)
plt.show()

​ 看起来很不错，能动(这里发现了init函数可以绘制下静态的大圆ln1，update函数只对动圆ln2的plot对象数据进行更新)：

​ 最后研究下旋轮线, 看看能否绘制出wiki页面上那个动画效果。先列出参数方程：
$$
选轮线参数方程：
\begin{cases}
x = r\cdot(t-\sin t) \\
y = r \cdot (1-\cos t)
\end{cases}
\\
圆心的坐标为:(t,r)
$$
​ 经过观察摸索，发现需要绘制3部分，一个是滚动的圆，一个是摆线，还有个圆心到绘制曲线的支点。坐标都可直接从参数方程推算出来，不多说，直接上代码和注释吧：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#def wheel_line():
fig = plt.figure(figsize=(8,2))
ax = plt.gca()
ax.grid()
ln, = ax.plot([], [], 'o-', color='g', lw=1) # 圆心连线 @center -> curve
circle, = ax.plot([], [], '-', color='b', lw=1) # 滚动的圆
curve, =  ax.plot([], [], '-', color='r', lw=1) # 摆线
curve_x, curve_y = [], [] 
r = 1
t = np.linspace(0, math.pi*2, 1000)
L = 4*np.pi*r
theta = np.linspace(0, L, 250)

def init():
    ax.set_xlim(-r, L + r)
    ax.set_ylim(0, L/4 + r/2)
    ln.set_data([0,0], [0,1])
    x_out = r*np.cos(t)
    y_out = r*np.sin(t) + r
    circle.set_data(x_out, y_out)
    return circle,ln

def update(frame):
    tt = theta[frame]    # 获取参数t
    x=r*(tt-np.sin(tt))
    y=r*(1-np.cos(tt))
    curve_x.append(x)
    curve_y.append(y)
    curve.set_data(curve_x, curve_y) # 更新摆线
    if i == len(theta) - 1:
        curve_x.clear()
        curve_y.clear()
    # update circle
    x_out = r*np.cos(t) + tt
    y_out = r*np.sin(t) + r
    circle.set_data(x_out, y_out)
    # new circle center @(tt,r)
    ln.set_data([tt,x],[r,y])
    return curve,circle,ln

ani = animation.FuncAnimation(fig, update, frames=range(len(theta)), init_func=init, interval=1)
ani.save('roll.gif', writer='imagemagick', fps=60)
plt.show()

​ 大功告成:

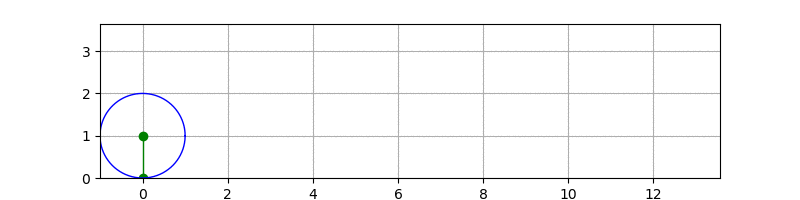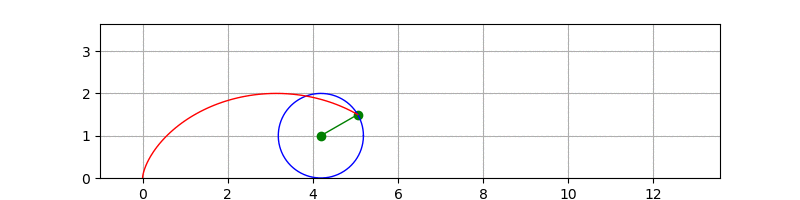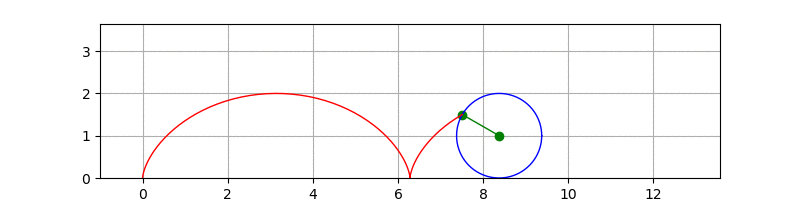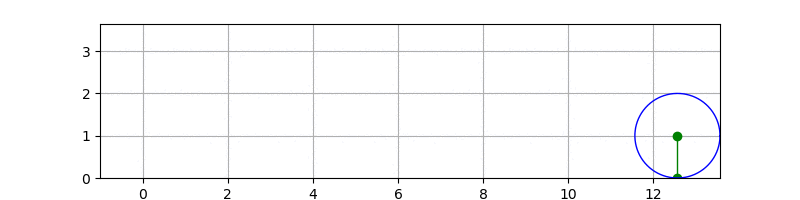
3 后记

​ 在摸索过程中，还是有很多坑需要注意的，最初那个摆线的例子，我没有计算好图形范围，画出来的圆是扁扁的，后来通过改figsize和ax.set_xlim/set_ylim为相同比例解决的；保存动画那个ani.save('roll.gif', writer='imagemagick', fps=60)总是报错，经过查找资料，解决方案是安装imagemagic，下载安装后第2节的例子都能顺利保存动图为gif。还有需要注意是的save函数里面的fps参数不能调太低，否则会出现动画卡顿的现象，太高又会出现动画速度很快的问题，这个参数需要配合frames即动画的总帧数，以及FuncAnimation里面的interval帧间隔时间参数(单位是ms)，总动画时间(秒)公式为：$frames * interval/1000+frames/fps$。
​ 读完这篇文章，相信绘制参数方程和动画不是一件难事吧:smile:。