Dynamic Programming

​ Dynamic programming is a math method for some special problems^1,for any $n$ ,the problem can be reduce to sub problems recursively.the Fibonacci is a typical DP problem:

$$ fib(n) = fib(n-1) + fib(n-2) $$

​ For a positive integer $n$ the result $fib(n)$ can be parted into two sub problems $fib(n-1)$ and $fib(n-2)$; for $n=0,1$ the result is 1 :

fib n
    | (n == 0) = a
    | (n == 1) = b
    | otherwise = fib (n - 1) + fib (n - 2)
    where a = 1; b = 1

​ or a more complex version:

fibs = 1 : 1 : zipWith (+) fibs (tail fibs) -- zipWith (x:xs) xs

1. A simple example

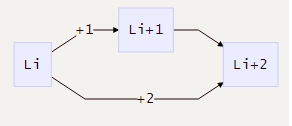
​ Suppose we have a ladder with $n$ steps, you can climb up one or two steps at one time, then how many method to reach the top of the ladder?^2

​ This problem has lots of similar version, one of them is : we have a string with $n$ 1s:’111…1’, give a encoding method, $a$ denotes ‘1’ and $b$ denotes ‘11’, find the methods to encode this string.
$$
S_n=\underbrace{1…1}\\
\qquad\;n\\
Encode(S_n)=\begin{cases}
a…,\quad’1’ \quad concat\quad Encode(S_{n-1})\\
b…,\quad’11’\quad concat\quad Encode(S_{n-2})\
\end{cases}
$$

​ The key to solve these problems are decompose the original $n$-th problem into sub-problems, for the first one, we denote the solution for $n$ as $L(n)$. if we stand at the $n$-th step of the ladder, we can only access there from $n-2$-th by climb 2 steps or $n-1$-th by climb 1 step; So we get $L(n) = L(n-1)+L(n-2)$, some thing looks familiar? yes, that is just a Fibonacci function!

​ Obviously,The second problem is also a Fibonacci.

2 Generate Permutations

​ In this part ,we want to generate all permutation for a positive integer $n$,not just getting the number of permutations:

$$P_n=n!$$

​ First, suppose we already get the solution for $n-1$ permutations $Perm(n-1)$ ,we can just insert the $n$ into all possible position to generate the $n$ permutations, for example:

$$
\begin{align}
Perm(2)&=[[1,2],[2,1]]\\
Perm(3)&=\begin{cases}
insert\space ‘3’\space into\space[1,2]=>[[3,1,2],[1,3,2],[1,2,3]]\\
insert\space ‘3’\space into\space[2,1]=>[[3,2,1],[2,3,1],[2,1,3]]\\
\end{cases}\\
&finally,\\
Perm(3)&=[[3,1,2],[1,3,2],[1,2,3]] + [[3,2,1],[2,3,1],[2,1,3]]
\end{align}
$$
​ So $Perm(n)$ can be decomposed by inserting $n$ for all $Perm(n-1)$’s children.Here we can also checking the number of permutations, given the number of $Perm(n-1)$ is $P_{n-1}=(n-1)!$, for each child we can insert $n$ at n positions(head or after $n-1$ numbers),so $P_n = n\cdot P_{n-1} = n!$,it’s the first equation of this part.

​ Haskell implement as following:

import Data.List hiding (permutations)
insert_loop x [] = [[x]]
insert_loop x (x':xs) = (x:x':xs):[x':xs'|xs'<-insert_loop x xs]

permutation [] = [[]]
permutation (x:xs) = concat [insert_loop x perm|perm <- permutation xs]

2 Sum of combinations

​ From math lectures in high school, we known this combination formula:
$$
\sum_{i=0}^n C_n^i = 2^n, n >=1\quad\quad(1)
$$
​ here is a simple prove:
$$
\because C_{n+1}^i(Choose\space i\space items\space from\space n \space items) =
\begin{cases}
C_n^{i-1} (Choose\space i-1\space items\space from \space first\space n\space items,then\space append\space the\space last\space one)\\
C_n^{i}(Choose\space i\space items\space from \space first\space n\space items)\\
\end{cases}\\
\\
\therefore C_{n+1}^i=C_{n}^i+C_{n}^{i-1}\quad \quad(2)\\
for\space n=1,the\space formula(1)\space is\space obvious.\\
suppose\space the\space formula(1)\space is\space right\space for\space n:\sum_{i=0}^{n}C_{n}^i+C_n^{n+1}=2^n;\\
we\space check\space the\space n+1:\\
\sum_{i=0}^{n+1} C_{n+1}^{i} = \sum_{i=0}^{n+1}(C_{n}^i+C_{n}^{i-1})
=\sum_{i=0}^{n+1}C_{n}^i +\sum_{i=0}^{n+1}C_{n}^{i-1}\\
for\space the\space first\space part\space above,\sum_{i=0}^{n+1}C_{n}^i=\sum_{i=0}^{n}C_{n}^i+C_n^{n+1}=2^n\\
for\space the \space second\space part,let \space j = i-1(j=0…n),we\space get:\\
\sum_{i=0}^{n+1}C_{n}^{i-1}=\sum_{i=1}^{n+1}C_{n}^{i-1}=\sum_{j=0}^{n}C_{n}^{j}=2^n\\
\therefore \sum_{i=0}^{n+1} C_{n+1}^{i}=2^n+2^n=2^{n+1}\\
\blacksquare QED.
$$

​

---